Calcul volumes 5°
 |
I. Quotient égaux
II. Fractions égales
III. Applications des fractions égales.
IV. Fractions et nombres entiers.
V. Comparer des fractions.
Intro
Unités de volumes
♦ Unités de volumes.
|
Définition : Le volume est la mesure de l’intérieur d’un solide. L'unité de mesure des volumes est le mètre-cube, on le note m3, c'est le volume d’un cube de 1 m d’arête. ♦ 1 m3 est le volume d’un cube de 1 m d’arête. ♦ 1 m3 est le volume d’un cube de 1 m d’arête. ♦ 1 m3 est le volume d’un cube de 1 m d’arête.
|
♦ Convertir des unités de volumes.
Propriété :
Dans un cube de 1dm d’arête, on peut ranger 10 x 10 x 10 = 1000 cubes de 1cm d’arête. donc 1 dm3 = 1000 cm3
Outils : Convertisseurs d'unités de volumes
Contenance
♦ Unités de contenance.
|
Définition :
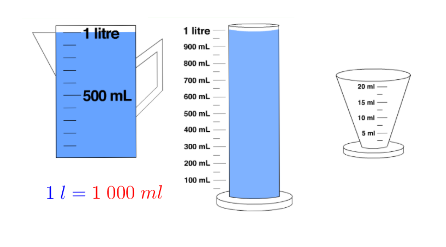
L’unité de contenance de référence est le litre. On la note L.
|
|
Outil : Convertisseur d'unités de contenance
♦ Unités de contenance vs unités de volumes.
Propriété :
1 L est la contenance d’un cube de 1 dm d’arête, donc 1 L = 1 dm3.
Point Méthode : Convertir des unités de volumes et des unités de contenance.
Volume pave
Propriété : Le volume d'un parallélépipède rectangle est donné par la formule :
Volume du parallélépipède = Longueur x largeur x Hauteur
Remarque :
Attention, il est necessaire que les longueurs soient exprimées dans la même unité de longueur pour pouvoir appliquer la formule.
Point Méthode : Calculer le volume d'un pavé droit.
Volume prisme
Propriété : Le volume d'un prisme droit est donné par la formule :
Volume = Aire base × Hauteur
Point Méthode : Calculer le volume d'un prisme droit.
Volume cylindre
Propriété : Le volume d'un prisme droit est donné par la formule :
Volume = Aire base × Hauteur
Point Méthode : Calculer le volume d'un prisme droit.
Formulaire
Les savoir faire du parcours
 |
Les savoir-faire du Chapitre : Solides. |
♦ Savoir décrire un solide.
♦ Savoir reconnaitre un solide.
♦ Savoir reconnaitre des solides représentés en perspective cavalière.
♦ Savoir reconnaitre le patron d'un solide.
♦ Savoir construire le patron d'un cube.
♦ Savoir construire le patron d'un parallélépipède rectangle.
♦ Savoir construire le patron d'un prisme droit.
♦ Savoir construire le patron d'un cylindre.
♦ Savoir calculer l'aire latérale d'un prisme droit.
♦ Savoir calculer l'aire latérale d'un cylindre.