volumes
s
 |
Calculer des volumes. |
I. Unités de volume.
II. Unités de contenance.
III. Volumes et contenances.
IV. Calculs du volume de solides particuliers
♦ Volume d'un cube.
♦ Volume d'un pavé droit.
V. Formulaire.
cubes 1
cubes 2
cubes 3
volumes
♦ Unités de volumes.
|
Définition :
Le volume est la mesure de l’intérieur d’un solide. L'unité de mesure des volumes est le mètre cube, on le note $m^3$, c'est le volume d’un cube de $1\;m$ d’arête. On note : ♦$1\;dm^3$ le volume d’un cube de $1\;dm$ d’arête. ♦$1\;cm^3$ le volume d’un cube de $1\;cm$ d’arête. ♦$1\;mm^3$ le volume d’un cube de $1\;mm$ d’arête. |
♦ Convertir des unités de volume.
|
Propriété :
|
Dans un cube de $1\; dm$ d’arête, on peut ranger $10 × 10 ×10 = 1\,000$ cubes de $1\;cm$ d’arête.
On en déduit que : $1 \;dm^3 = 1\,000 \;cm^3$
|
Outil :
|
Convertisseur d'unités de volume. |
contenace
|
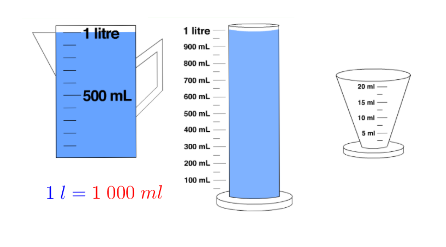
Définition :
L’unité de contenance de référence est le litre. On la note $L$. |
|
|
Outil :
|
Convertisseur d'unités de contenance |
vol vs cont
|
Propriété :
|
$1\; L$ est la contenance d’un cube de $1 \;dm$ d’arête, donc $1\; L = 1 \;dm^3$.
|
Méthode :
|
Convertir des unités de volume en unités de contenance. |
cube
|
Propriété :
|
Le volume d'un cube de longueur d'arête $c$ est donné par la formule :
$\mathcal{V}_{cube} =c×c×c$
|
Méthode :
|
Calculer le volume d'un cube. |
pave
|
Propriété :
|
Le volume d'un parallélépipède rectangle de Longueur $L$, de largeur $l$ et de hauteur $h$ est donné par la formule :
$\mathcal{V}_{parallélépipède} =L×l×h$
Remarque :
Attention, il est nécessaire que toutes les longueurs soient exprimées dans la même unité de longueur pour pouvoir appliquer la formule.
|
Méthode :
|
Calculer le volume d'un parallélépipède rectangle. |
formulaire
Attention :
Avant d'appliquer une formule pour calculer un volume il faut s'assurer que toutes les longueurs sont exprimées dans la même unité.
| $\mathcal{V}_{cube}=c×c×c=c^3$ | $\mathcal{V}_{pavé}=l×L×h$ |
sf
 |
Les savoir-faire du Chapitre : Calculs de volumes. |
♦ Savoir convertir des unités de volume.
♦ Savoir convertir des unités de contenance.
♦ Savoir utiliser la relation entre unités de volume et unités de contenance.
♦ Savoir calculer le volume d'un cube.
♦ Savoir calculer le volume d'un parallélépipède rectangle.
♦ Savoir résoudre un problème de volume.